中医入门
最近一直在断断续续学习中医。
学中医的原因有很多:
- 带小孩子(两岁多)去医院看病,排队、抽血、输液、拿药。小孩子闹,医生忙,医院人多的都没地方坐着输液。呵呵!
- 步入中年之后,上有老下有小,不可能有啥风吹草动都跑去医院。现在的医院人太多,而且太“冰冷”。
- 不想把血汗钱都交给医院。病了之后、老了之后希望能有尊严的活着。
再有就是我心目中的中医一直很厉害,只是现在传承出了问题。好中医很少,能遇到的就更少了。
所以就自己学,不要把世界让给那些你讨厌的人。
- 慢慢学习之后,发现中医没有想象中的那么难,反而很吸引人。
- 现在平常的小病都是自己想办法解决,网上买药或者买药材自己熬。
- 很多药还能直接做到家常菜里,好吃又能调理身体。
正所谓:“上以疗君亲之疾,下以救贫贱之厄,中以保身长全,以养其生。” —— 【汉】张仲景《伤寒论·序》
中医入门
我自己学习了解下来,最终选择以《伤寒论》为代表的经方学派。
这里整理记录一下自己的入门道路:
首先:看完这两个倪师(倪海厦)珍贵视频,先有个整体的理解。倪师讲课不枯燥,很吸引人。大部分都能不知不觉听完。
然后:剩下就是自学、自用。当有效果的时候,就是对你最好的嘉奖。
附录:
倪海厦,籍贯中国台湾。1954 年出生,2012 年 1 月 31 日去世,享年 59 岁。(倪师在 1994 年教授《天纪》的视频中有讲过自己 59 岁是大小二限逢,是大劫)
自学中医入门,后拜师学艺,所学甚广。是少数的 山、医、命、卜、相 (堪舆、中医、命理、占卜、面相)都比较精通的鬼才。25 岁左右给人算卦,之后移民去美国,于 1989 年(35 岁)开始在美国开设汉唐中医诊所,行医 20 余年。于 1995 年创办汉唐中医学院以培育和储蓄中医人才,传承经方医学。编撰并教授了 《天纪》、《人纪》系列,《地纪》还未完成就已去世。
推荐的书籍、资料
现在是信息大爆炸时代,从来都不缺学习资料。缺的只是热爱学习的心。
这里推荐一个很好用的网站:中医世家 。各种资料非常齐全,可以在线看,也可以直接下载之后离线查看。
视频:
B 站资源比较多。可以先看热心网友们上传的倪海厦系列视频。其他可以自行搜索查看。
倪海厦是非常注重学习顺序的,如果单看中医的内容的话,他的观点是:先学针灸大成,然后是黄帝内经,再学神农本草经,再学伤寒论,最后学金匮要略。
理论:
- 《黄帝内经》:能看一辈子,每次看都有新的理解
- 《难经》:黄帝内经的补充内容。字数很少,可以解惑。
- 《外经微言》清 陈士铎 :也叫皇帝外经。黄帝内经的补充内容。医力深厚,文笔很好,可以解惑。
症状、方剂:
- 《伤寒杂病论》汉 张仲景:真正能用的书;看过之后,可以当字典,常看常新。
- 《辨症玉函》清 陈士铎
- 《石室秘录》清 陈士铎
针灸、药剂:
- 《针灸甲乙经》 晋 皇甫谧编,黄龙祥整理。人民卫生出版社
- 《本草新编》清 陈士铎
课外读物:
- 《医本正经》:偏散文的另类中医图书。作者:懒兔子(同名微信公众号)。我是这本书入的中医。我和作者有点同感,家中长辈去世的时候我刚上中学,懵懂未知,只觉伤心。这本书里作者提了很多自己阅读的其他中医书籍,我也就越读越多,一发不可收拾了。
- 《思考中医》 刘力红 著。刘力红:广西中医学院 医学博士,教授。致力推动真正中医的发展。早年请倪海厦去给他带的研究生们讲课。
- 《霹雳大医-李可》 张存悌 卓同年 著。李可:传奇老中医,善用附子,从 ICU 救回了很多人。自创中药方 28 首,其中“破格救心汤”尤为著名。李可一生致力于弘扬和振兴中医事业,于 2013 年 2 月 7 日去世,享年 83 岁。
言论:
- 我们只需尽力去做,功过是非,任由后人评说。 —— 李可
- 一个人一定要保持一颗安静、清净的心,才能明白《内经》、《难经》、《本经》及《伤寒杂病论》里所蕴含的天地规律和自然法则并加以应用。 —— 李可
- 尝思用药如用兵。善用兵者必深知将士之能力,而后可用之以制敌;善用药者亦必深知药性之能力,而后能用之以治病。—— 【清】张锡纯《医学衷中参西录》
- 人不穷理,不可以学医;医不穷理,不可以用药。——【清】陈士铎《洞天奥旨卷十六劝医六则》
- 读书而不临证,不可以为医。临证而不读书,亦不可以为医。 —— 【清】陆九芝《世补斋医书》
古代计量换算
根据已知的资料(经方家:陆九芝,傅青主;徒弟:陈士铎;近代:倪海厦),伤寒论经方中所用计量换算如下:
汉制 一斤 = 汉制 16 两 ≈ 今制 60 克
汉制 半斤 = 汉制 八两 ≈ 今制 6 钱 ≈ 今制 30 克 (今制 1钱 = 5克)
汉制 一两 = (清制)经方 一钱 ≈ 今制 3.75 克
汉制 一升 = 经方 五钱 ≈ 今制 200 毫升
* 比如 半夏,古用 酒盅 来称,一盅叫一升。不是现在的1000毫升的意思。
* 再比如煎药时,以水七升 = 汉制 7 碗水 ≈ 今制 1400 毫升
特别说明,倪海厦所使用的为 台湾度量衡,换算如下:
一斤 = 600g = 十六两
一两 = 37.5g = 十钱
一钱 = 3.75g = 十分 (倪师视频里大部分都是用这个 钱 做单位)
另外的注意事项:
1. 一钱 取3克或4克 影响不大,可以根据患者体型、病况决定。一般的病症用3~5克,严重点的用9~12克,救命时用15克以上也没问题。
2. 最重要的是各个药物的使用比例。比例!比例!
3. 伤寒论经方大多一剂药是分几次服用的,所以看起来分量很大。实际换算下来每次服用的量都还好。
更新于 2023年11月30日
新的计量换算:
过去几个月又读了一些李可医生相关的书籍资料,发现一个新的计量换算标准,觉得是更正确的。这里记录一下。
《汉书·律历志》里面这样记载,“度者,分、寸、尺、丈、引也,所以度长短也……一龠容千二百黍,重十二铢,两之为两。二十四铢为两,十六两为斤,三十斤为钧,四钧为石。”
“光和大司农铜权”重 2996g,12斤权,折合为每斤249.7g。同理考证现藏上海博物馆的东汉“光和大司农铜斗”,得出东汉每升为200 ml。
汉承秦制,《伤寒论》《金匮要略》中的药物剂量应按此值折算,折合1斤为今之 250g,1两为 15.625g,1铢约 0.65g;1斗为今之 2000ml,1升为 200ml,1合为 20ml。(大枣 12 枚 ≈ 30g)
`医界共识:剂量问题是经方不传之秘`。剂量,是方药治病的核心一环,犹如将军的刀剑。
自1981年东汉度量衡器【大司农铜权】出土,证实了汉代一两等于现代15.625克,一斤等于250克,液体一升,等于200ml。这一重大发现,解决了古方剂量的一大疑案。李时珍之后400多年,以“古之一两,为今之一钱”,仅取经方原量的十分之一为临床应用的标准,显然是错了。
另外:宋代是我国度量衡的分水岭,一旦兼并一块疆土就会废除原有度量衡制度,推行统一制度。宋代药物的权重单位多以钱、分为主。从官修编订的《圣济总录》、《太平惠民和剂局方》可以看出,宋代的药量为历代最小。到了明清时期,尽管计量衡值还是有所增长,但计量制基本沿用宋代。而且宋代长期战乱,资源匮乏,所以流行煮散(药物先打碎,熬煮之后滤渣)的方式熬药,以节约药材。虽然计量变小,但是药性有所提升。
更新于 2024年7月10日
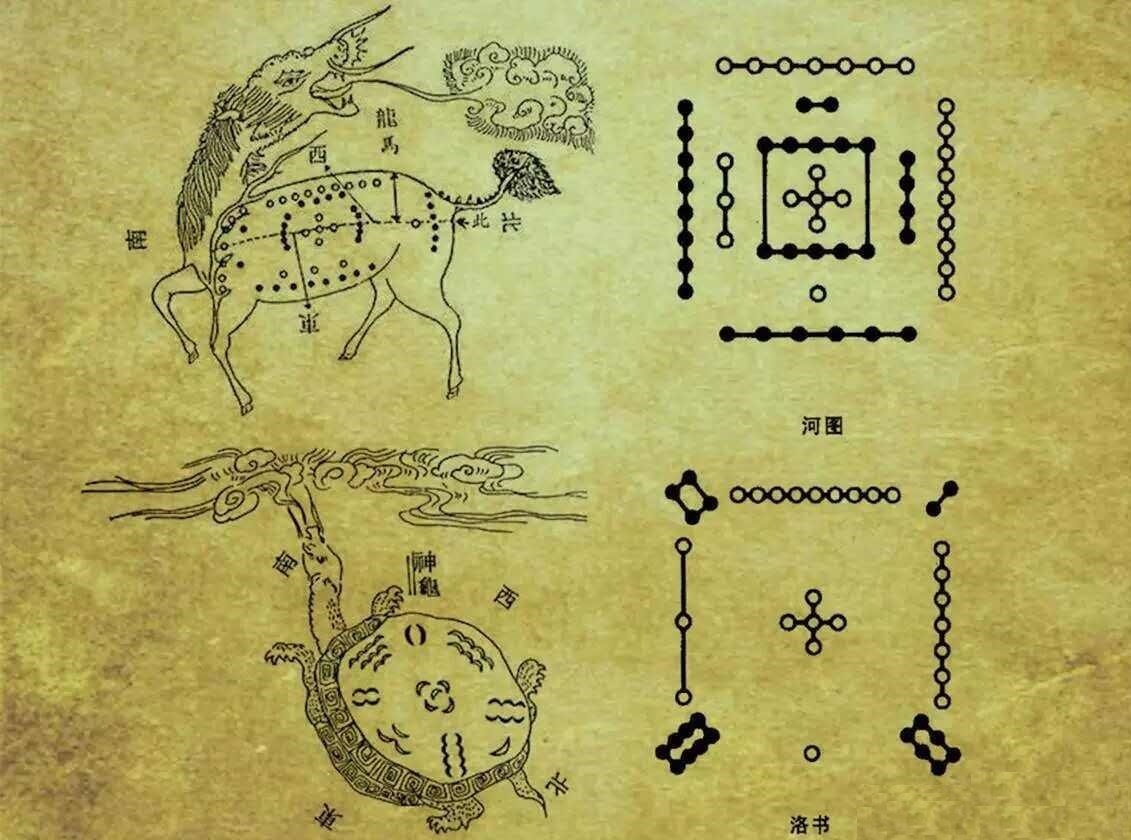
为啥放了个河图洛书的图
学习中医的过程中不可避免的会接触到非常多的古知识。
中医用的最多的是五行阴阳理论。随着书越读越多,自己也有了点感悟:五行对应五脏之后,每个脏腑都既包含阴又包含阳,而且每个里面的阴阳比例都不一样。如果比例是正常的,人就不会生病。中医也是通过药物去调整这个比例,让你的身体恢复正常的。
这个比例我感觉和河图洛书很像。
知乎上发现这个 回答,感觉不错。
自己也试着用 Python 把里面提到的 阿基米德螺旋线 给画了出来:
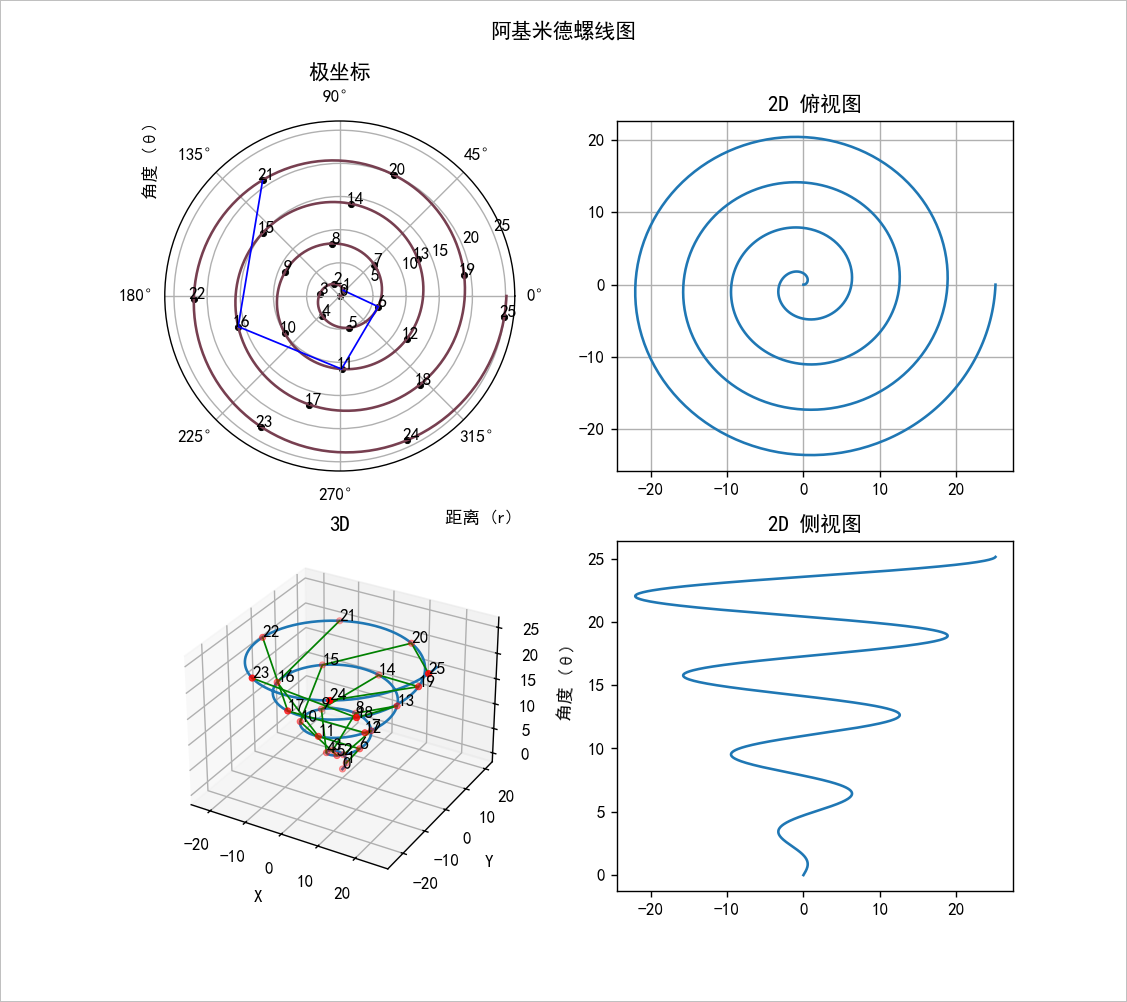
# 阿基米德螺旋线(Archimedean spiral),亦称“等速螺线”。
# 当一点P沿动射线OP以等速率运动的同时,这射线又以等角速度绕点O旋转,点P的轨迹称为“阿基米德螺线”。
# 这种螺线的每条臂的间距永远相等于 2πb
#
# 它的极坐标方程为:r = a + bθ
# 其中 a 为起始点与极坐标中心的距离,主要控制旋转整个螺线。从原点开始时 a=0 。
# 其中 b 为控制螺线间的距离, 因为 b = r / θ,所以 b 越大,变化越快。螺线相同角度下的半径 r 增长越快,图形越稀疏。
#
# 在 直角坐标系 下,利用极坐标到直角坐标的公式,可以得出:
# x = r * cosθ ; y = r * sinθ;
#
# 还可以通过加入 角速度ω 和 线速度v ,写成关于时间 t 的函数,控制生成的螺线形状:
# x = vt*cos(ωt) ; y = vt*cos(ωt)
#
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.pylab import mpl
mpl.rcParams["font.sans-serif"] = ["SimHei"] # 显示中文
mpl.rcParams["axes.unicode_minus"] = False # 显示负号
num_points = 1000
tickets = 9
size = 4 # 生成的螺旋个数
# 定义阿基米德螺旋线的函数 r = a + bθ
def Archimedes_Spiral(a, b, theta):
r = a + b * theta
return r
# 生成从 0 到 4π 的等间隔的角度数组。4π 会创建两个完整的螺旋
theta = np.linspace(0, size * 2 * np.pi, num_points)
# 使用定义的螺旋函数计算对应的半径
a, b = 0, 1
r = Archimedes_Spiral(a, b, theta)
# 在 直角坐标系 下,利用极坐标到直角坐标的公式 `x = r * cosθ ; y = r * sinθ` ,可以得出:
x = r * np.cos(theta)
y = r * np.sin(theta)
z = np.linspace(0, size * 2 * np.pi, num_points) # z = theta
fig = plt.figure(figsize=(9, 8))
fig.suptitle("阿基米德螺线图")
ax1 = fig.add_subplot(221, polar=True) # 极坐标下的阿基米德螺线图
ax2 = fig.add_subplot(222) # 直角坐标系下的螺线图
ax3 = fig.add_subplot(223, projection="3d") # 3D 阿基米德螺线图
ax4 = fig.add_subplot(224) #
######### 极坐标下的阿基米德螺线图 #########
ax1.set_title("极坐标")
ax1.plot(r, theta, color="#773f50")
ax1.grid(True) # 添加网格线
# 添加标签和标题
ax1.set_xlabel("距离 (r)", loc="right")
ax1.set_ylabel("角度 (θ)", loc="top")
# 在 r 的整数值附近 添加标签
x_int, y_int, r_int, z_int = [], [], [], []
for i in range(0, tickets * size):
for j in range(len(r)):
if r[j] > i:
x_int.append(x[j])
y_int.append(y[j])
r_int.append(r[j])
z_int.append(theta[j])
break
# 把 r 点数据分成五组:黑水、青木、赤火、黄土、白金,用线连起来
bline_x1, bline_x2, bline_x3, bline_x4, bline_x5 = [], [], [], [], []
bline_y1, bline_y2, bline_y3, bline_y4, bline_y5 = [], [], [], [], []
bline_r1, bline_r2, bline_r3, bline_r4, bline_r5 = [], [], [], [], []
bline_z1, bline_z2, bline_z3, bline_z4, bline_z5 = [], [], [], [], []
for i in range(1, len(x_int), 5):
bline_x1.append(x_int[i])
bline_y1.append(y_int[i])
bline_r1.append(r_int[i])
bline_z1.append(z_int[i])
if len(x_int) > (i + 1):
bline_x2.append(x_int[i + 1])
bline_y2.append(y_int[i + 1])
bline_r2.append(r_int[i + 1])
bline_z2.append(z_int[i + 1])
if len(x_int) > (i + 2):
bline_x3.append(x_int[i + 2])
bline_y3.append(y_int[i + 2])
bline_r3.append(r_int[i + 2])
bline_z3.append(z_int[i + 2])
if len(x_int) > (i + 3):
bline_x4.append(x_int[i + 3])
bline_y4.append(y_int[i + 3])
bline_r4.append(r_int[i + 3])
bline_z4.append(z_int[i + 3])
if len(x_int) > (i + 4):
bline_x5.append(x_int[i + 4])
bline_y5.append(y_int[i + 4])
bline_r5.append(r_int[i + 4])
bline_z5.append(z_int[i + 4])
ax1.plot(bline_r1, bline_z1, color="b", linewidth=1)
ax1.scatter(
r_int, z_int, s=[0.5 * len(r_int)], color="black", linewidth=0.5
) # 用红色显示整数点
for i in range(len(r_int)):
ax1.annotate(
str(int(r_int[i])),
xy=(r_int[i], z_int[i]),
textcoords="offset points",
xytext=(2, 0),
ha="center",
)
######### 直角坐标系下的螺线图 #########
ax2.set_title("2D 俯视图")
ax2.plot(x, y)
# plt.xticks(np.arange(0, max(x), step=1)) # 设置x轴刻度位置,这里以1为步长
ax2.grid(True)
######### 3D 螺线图 #########
ax3.plot(x, y, z)
# 设置轴标签和标题
ax3.set_xlabel("X")
ax3.set_ylabel("Y")
ax3.set_zlabel("角度 (θ)")
ax3.set_title("3D")
ax3.plot(bline_x1, bline_y1, bline_z1, color="green", linewidth=1)
ax3.plot(bline_x2, bline_y2, bline_z2, color="green", linewidth=1)
ax3.plot(bline_x3, bline_y3, bline_z3, color="green", linewidth=1)
ax3.plot(bline_x4, bline_y4, bline_z4, color="green", linewidth=1)
ax3.plot(bline_x5, bline_y5, bline_z5, color="green", linewidth=1)
# 用红色显示整数点
ax3.scatter(x_int, y_int, z_int, s=[0.5 * len(r_int)], color="r", linewidths=0.5)
for i in range(len(r_int)):
ax3.text(
x_int[i],
y_int[i],
z_int[i],
str(int(r_int[i])),
)
######### 2D 螺线图 #########
ax4.set_title("2D 侧视图")
ax4.plot(x, z)
# plt.xticks(np.arange(0, max(x), step=1)) # 设置x轴刻度位置,这里以1为步长
ax4.grid(False)
# plt.tight_layout()
plt.show()